 ,若
,若 在
在 上恒成立,则实数
上恒成立,则实数 的取值范围是( )
的取值范围是( )一、选择题
1.
已知 ,若
,若 在
在 上恒成立,则实数
上恒成立,则实数 的取值范围是( )
的取值范围是( )
A. B.
B. C.
C. D.
D.
2.
设f(x)是定义在R上的偶函数,且当 时,
时, ,若对任意的
,若对任意的 ,不等式
,不等式 恒成立,则实数m的最大值是( )
恒成立,则实数m的最大值是( )
A.-1 B. C.
C.  D.
D.
3.
水以恒速(即单位时间内注入水的体积相同)注入下面的容器中,则此容器里水的高度 与时间t的函数关系图象是( )
与时间t的函数关系图象是( )

4.
如图所示,阴影部分的面积S是h的函数( ),则该函数的图象是( )
),则该函数的图象是( )





A. B. C. D.
5.
函数 的零点所在的一个区间是( )
的零点所在的一个区间是( )
A.(-1,0) B.(0,1) C.(1,2) D.(2,3)
6.
已知函数 ,则
,则 ( )
( )
A. B.
B. C.3 D.-3
C.3 D.-3
7.
函数 的零点个数为( ▲ )
的零点个数为( ▲ )
A.0 B.1C.2 D.3
8.
已知函数f(x)满足 ,则函数f(x)的图象不可能发生的情形是( )
,则函数f(x)的图象不可能发生的情形是( )

A B C D
9.
已知函数 (其中
(其中 ),对于不相等的实数
),对于不相等的实数 ,设
,设 ,
, ,现有如下结论:①对于任意不相等的实数
,现有如下结论:①对于任意不相等的实数 ,都有
,都有 ;②存在实数a,对于任意不相等
;②存在实数a,对于任意不相等 ,都有
,都有 ;③当
;③当 时,存在不相等的实数
时,存在不相等的实数 ,使得
,使得 ,其中正确的是( )
,其中正确的是( )
A.① B.①② C.②③ D.①③
10.
设函数 ,则下列结论错误的是( )
,则下列结论错误的是( )
A.f(x)的值域为{-1,1} B.f(x)是非奇非偶函数
C.对于任意 ,都有
,都有 D.f(x)不是单调函数
D.f(x)不是单调函数
二、填空题
11.
已知函数 ,
, ,若方程
,若方程 有且只有三个不同的实数根,则实数a的取值范围是 .
有且只有三个不同的实数根,则实数a的取值范围是 .
12.
已知关于x的方程 在(-2,+∞)上有3个相异实根,则实数a的取值范围是 .
在(-2,+∞)上有3个相异实根,则实数a的取值范围是 .
13.
设 ,则
,则 的最大值为 .
的最大值为 .
14.
已知 ,要使函数
,要使函数 在区间[0,4]上的最大值是9,则m的取值范围是 .
在区间[0,4]上的最大值是9,则m的取值范围是 .
15.
已知定义在R上的函数f(x)恒满足 ,且f(x)在[1,+∞)为单调减函数,则当
,且f(x)在[1,+∞)为单调减函数,则当 时,f(x)取得最大值;若不等式
时,f(x)取得最大值;若不等式 成立,则m的取值范围是 .
成立,则m的取值范围是 .
16.
关于x的方程 ,给出下列四个判断:
,给出下列四个判断:
①存在实数k,使得方程恰有4个不同的实根;
②存在实数k,使得方程恰有5个不同的实根;
③存在实数k,使得方程恰有6个不同的实根;
④存在实数k,使得方程恰有8个不同的实根;
其中正确的为___ ▲ ___(写出所有判断正确的序号).
三、解答题
17.
已知函数f(x)对任意实数x,y恒有 且当
且当 ,
, ,又
,又 .
.
(1)判断函数f(x)的奇偶性,并证明你的结论;
(2)若任意 ,不等式
,不等式 成立,求实数m的取值范围;
成立,求实数m的取值范围;
(3)若 求实数n的取值范围。
求实数n的取值范围。
18.
已知函数 ,其中
,其中 .
.
(1)判断并证明函数f(x)的奇偶性;
(2)判断并证明函数f(x)在(-4,4)上的单调性;
(3)是否存在这样的负实数k,使 对一切
对一切 恒成立,若存在,试求出k取值的集合;若不存在,说明理由.
恒成立,若存在,试求出k取值的集合;若不存在,说明理由.
19.某医药研究所开发的一种药,如果成年人按规定的剂量服用,据监测,服药后每毫升中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.(当 时,
时, )
)
(Ⅰ)写出第一次服药后y与t之间的函数关系式 ;
;
(Ⅱ)据进一步测定,每毫升血液中含药量不少于0.25微克时,治疗疾病有效,求服药一次后治疗疾病有效时间.

20.
(本小题12分)
近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司“Mobike”计划在甲、乙两座城市共投资120万元,根据行业规定,每个城市至少要投资40万元,由前期市场调研可知:甲城市收益P与投入a(单位:万元)满足 ,乙城市收益Q与投入a(单位:万元)满足
,乙城市收益Q与投入a(单位:万元)满足 ,设甲城市的投入为x(单位:万元),两个城市的总收益为f(x)(单位:万元)。
,设甲城市的投入为x(单位:万元),两个城市的总收益为f(x)(单位:万元)。
(1)当甲城市投资50万元时,求此时公司总收益;
(2)试问如何安排甲、乙两个城市的投资,才能使总收益最大?
21.
已知函数 .
.
(1)当 ,
, 时,求满足
时,求满足 的
的 的值;
的值;
(2)若函数f(x)是定义在R上的奇函数.
①存在 ,使得不等式
,使得不等式 有解,求实数k的取值范围;
有解,求实数k的取值范围;
②若函数 满足
满足 ,若对任意
,若对任意 且
且 ,不等式
,不等式 恒成立,求实数m的最大值.
恒成立,求实数m的最大值.
试卷答案
1.B
2.B
3.C
4.
A
观察图,可知阴影部分的面积S随h的增大而减小, 排除B和C.
排除B和C.
由于图形的宽度上小下大,所以S的变化率随h的增大而减小, 排除D.
排除D.
故选A.
5.
D
因 ,则函数
,则函数 零点所在的区间是
零点所在的区间是 ,应选答案D.
,应选答案D.
6.
B
由题可知, ,
,

故选B.
7.D
8.
C
将选项C第三象限的图像向右平移一个单位再作关于 轴对称所得的图像不与第一象限的原图像重合,反之其它选项的图像可以,故C错误,应选C.
轴对称所得的图像不与第一象限的原图像重合,反之其它选项的图像可以,故C错误,应选C.
9.
D
 表示函数
表示函数 图象上任意两点连线的斜率,同理
图象上任意两点连线的斜率,同理 表示函数
表示函数 图象上任意两点连线的斜率.由于
图象上任意两点连线的斜率.由于 是减函数,所以①正确;
是减函数,所以①正确; 左减右增,所以②错误;由于两个函数图像有两个交点,此时这两个交点连线斜率相同,故③正确.
左减右增,所以②错误;由于两个函数图像有两个交点,此时这两个交点连线斜率相同,故③正确.
10.
B
A:由函数性质可知, 的值只能取1,-1,所以值域为
的值只能取1,-1,所以值域为 ,正确;
,正确;
B:当 为有理数时,
为有理数时, 也是有理数,则
也是有理数,则 ;同理可得,当
;同理可得,当 为无理数时,也满足
为无理数时,也满足 ,所以
,所以 时,均有
时,均有 ,为偶函数,错误;
,为偶函数,错误;
C:当 为有理数时,
为有理数时, 也是有理数,则
也是有理数,则 ;同理可得,当
;同理可得,当 为无理数时,也满足
为无理数时,也满足 ,所以
,所以 时,均有
时,均有 ,正确;
,正确;
D:由函数性质易知, 不是单调的,正确;
不是单调的,正确;
故选B。
11. 
12.

∵方程 在
在 上有3个相异实根,
上有3个相异实根,
∴函数 与
与 的图象在
的图象在 上有三个不同交点,
上有三个不同交点,
在坐标系中画出函数的图象,由图象可知,在 上,函数
上,函数 与
与 有两个不同的交点,在
有两个不同的交点,在 上,函数
上,函数 与
与 有一个交点
有一个交点
∵  ,
,
联立 ,整理得
,整理得 ,
,
∴  ,即
,即 ,解得
,解得
∴实数a的取值范围为

13.
1
由 ,解得
,解得 或
或

 ,
,

 ,
,
函数图象如图所示,当 时取得最大值1.
时取得最大值1.
故答案为1.

14.

不等式即: ,等价于:
,等价于:

结合函数的定义域可得: ,
,
据此可得: ,
,
即 的取值范围是
的取值范围是 .
.
15.
1,(0,2)
由 可知,
可知, 存在对称轴
存在对称轴 ,又
,又 在
在 单调递减,则
单调递减,则 在
在 单调递增,所以
单调递增,所以 ,
, 取到最大值;
取到最大值;
由对称性可知,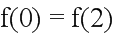 ,
,
所以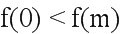 ,得
,得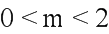 ,即
,即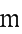 的范围为
的范围为 。
。
16.
①②③
17.
(1)在条件中,令x=y=0,则f(0)=2 f(0),∴ f(0)=0 ……………1分
再令y=-x,则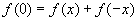 ; …………………………………2分
; …………………………………2分
故f(-x)=f(x),f(x)为奇函数. ……………………………3分
(2)解:设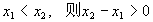 ,∵当
,∵当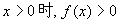 ,∴
,∴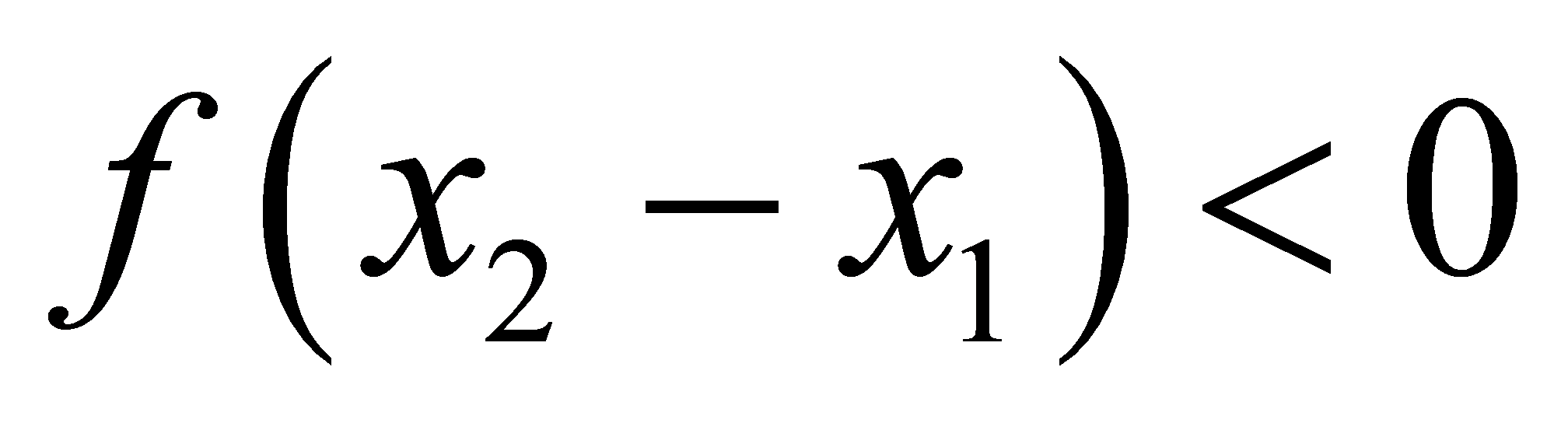 ,
,
∵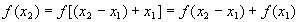 ,………………………4分
,………………………4分
∴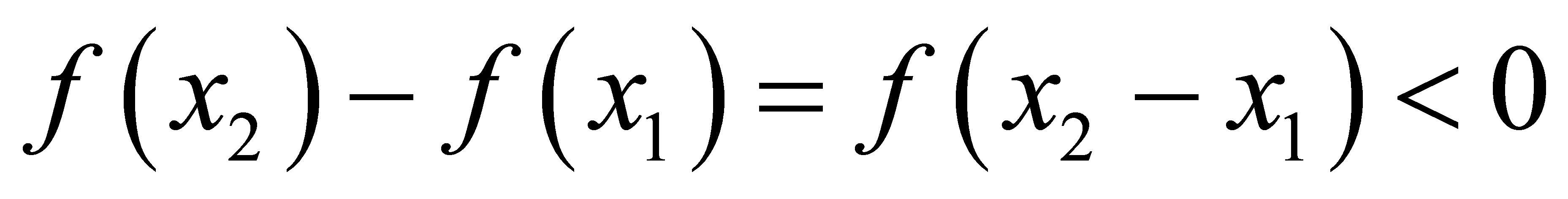 ,即
,即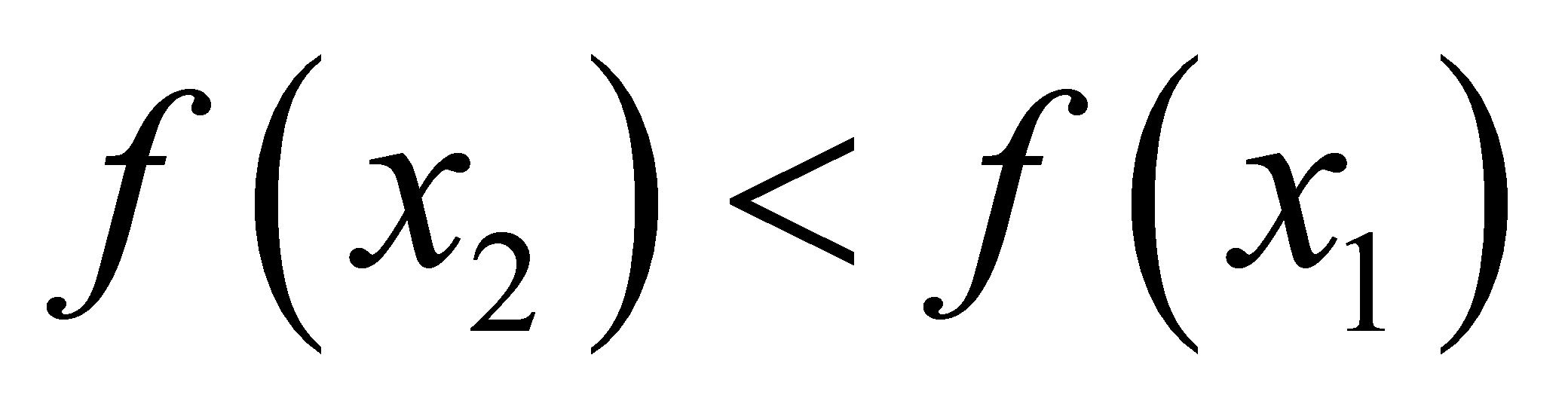 ,
,
∴f(x)为减函数. ……………………………5分
∴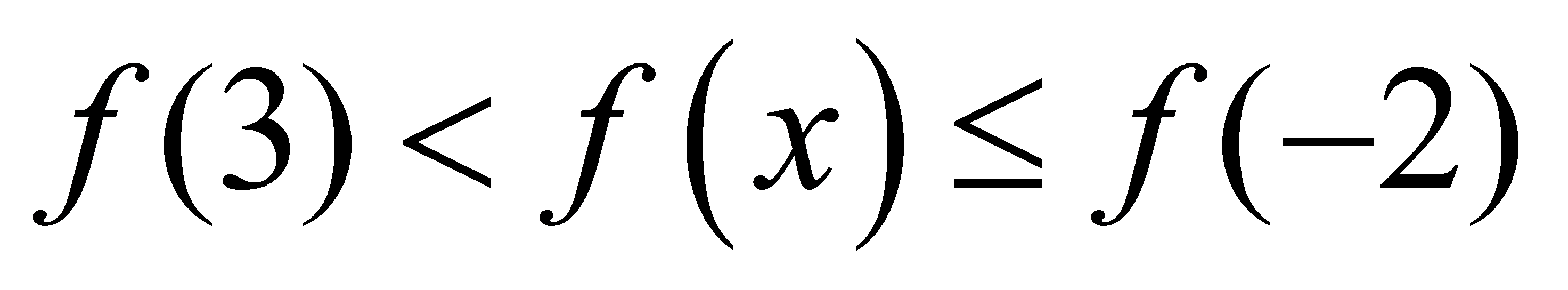
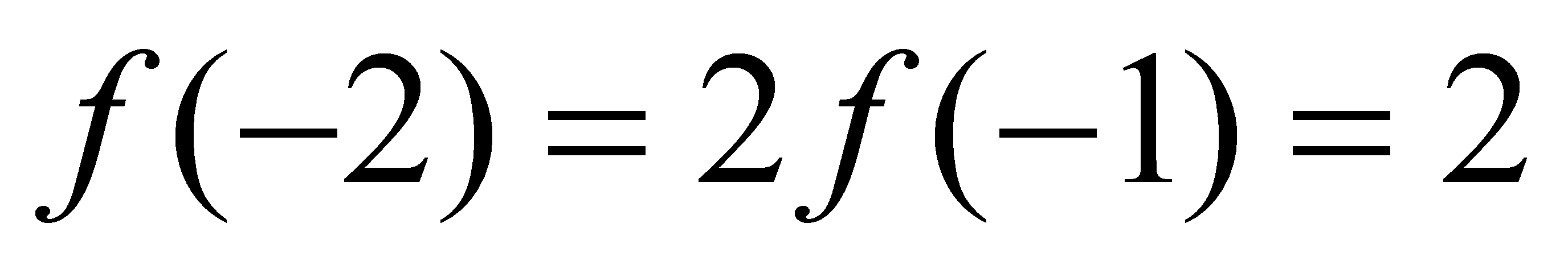 ,
,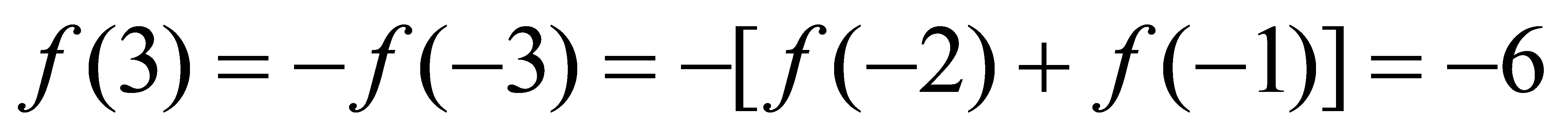 ………………………6分
………………………6分
∴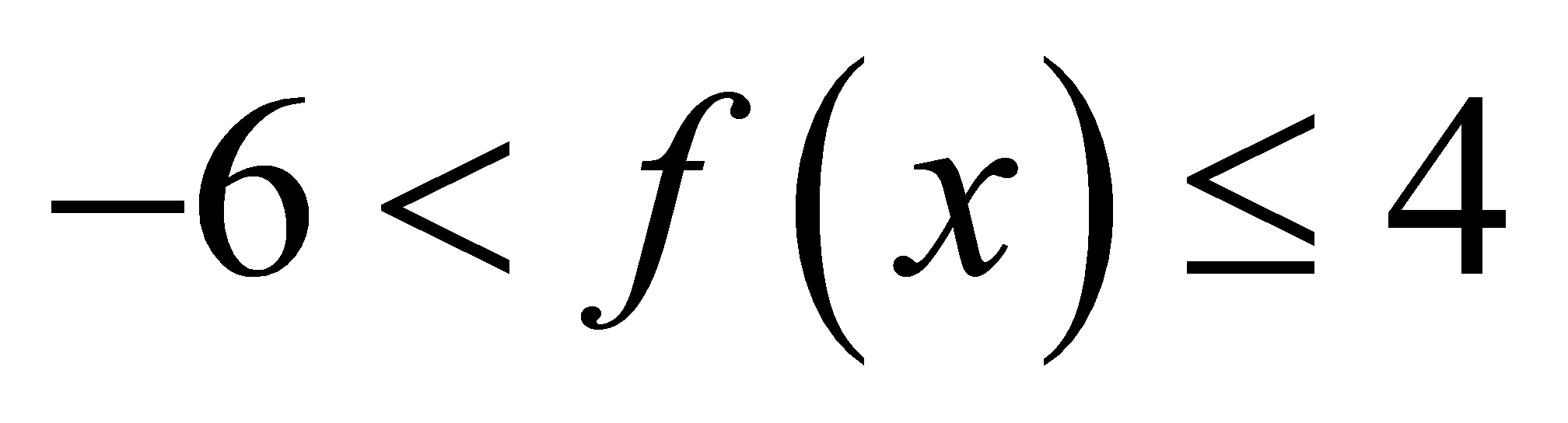
若任意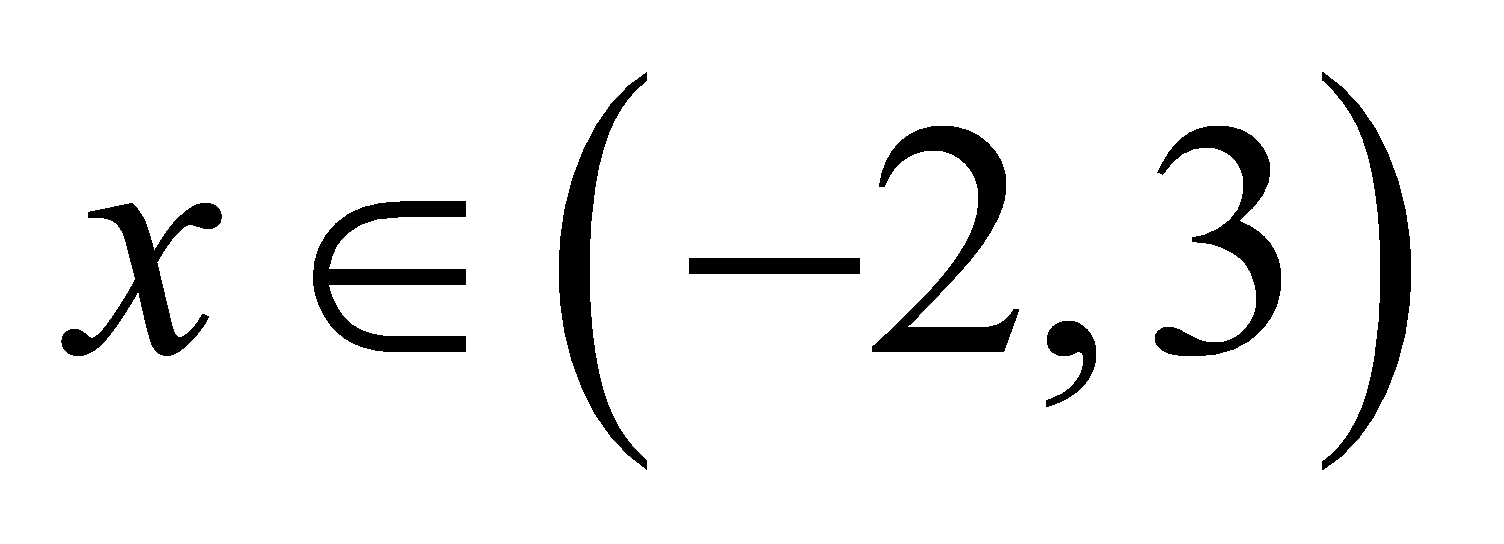 ,不等式
,不等式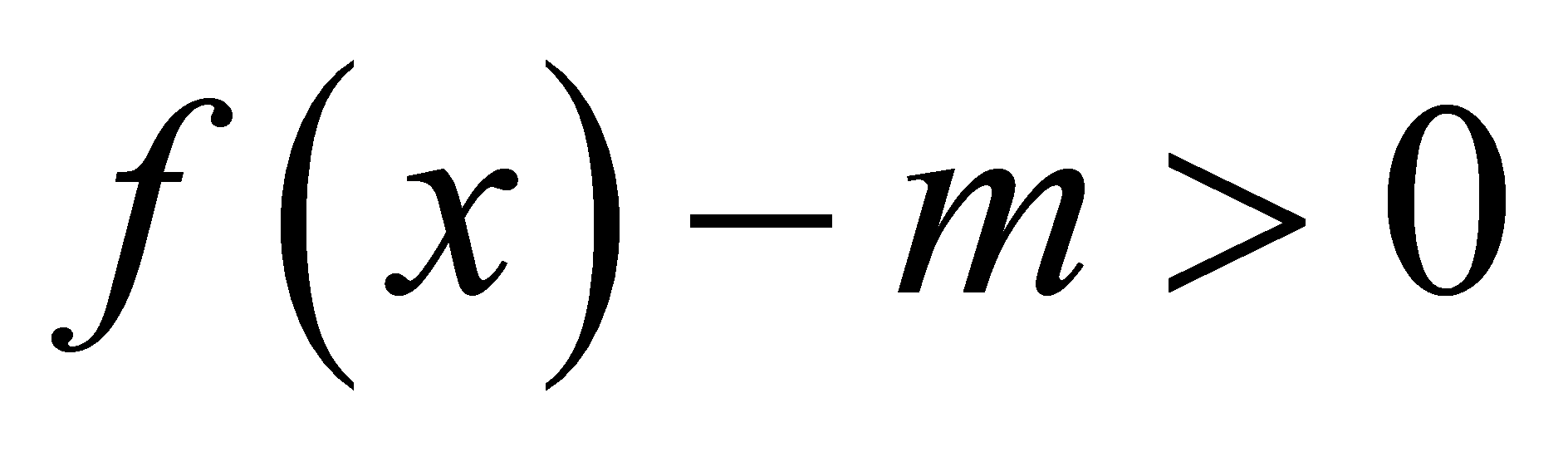 成立
成立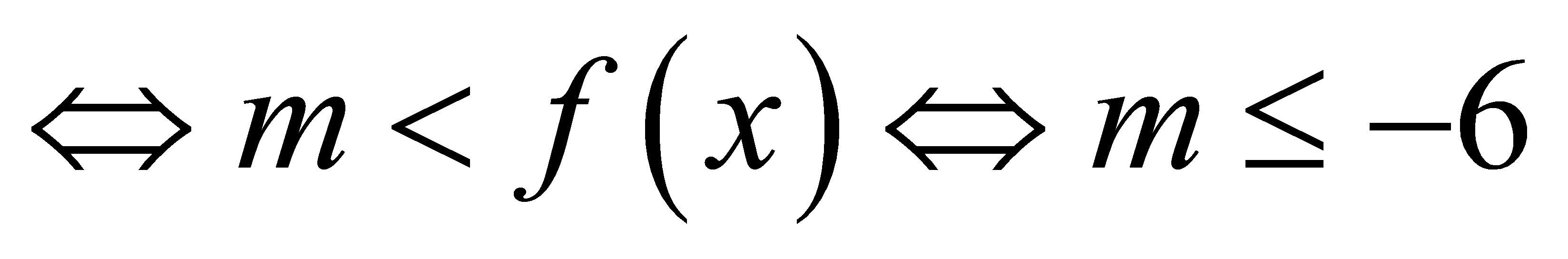 ………7分
………7分
(3)由(2)知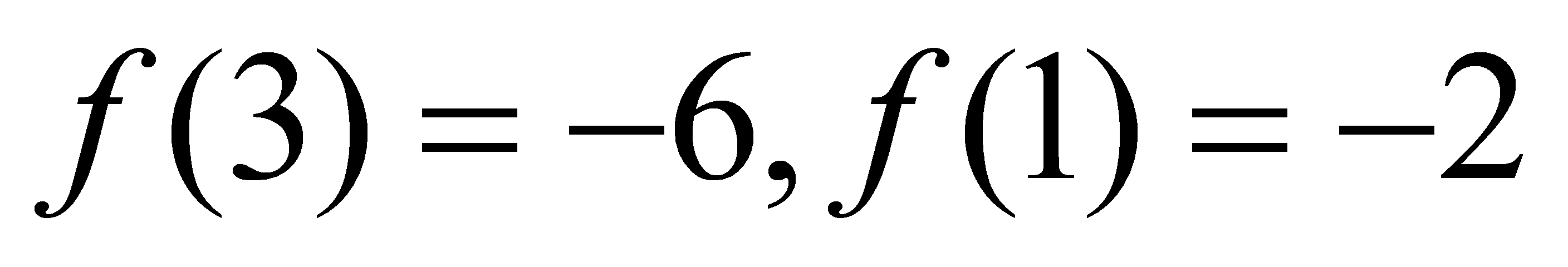 ,则
,则 ,所以
,所以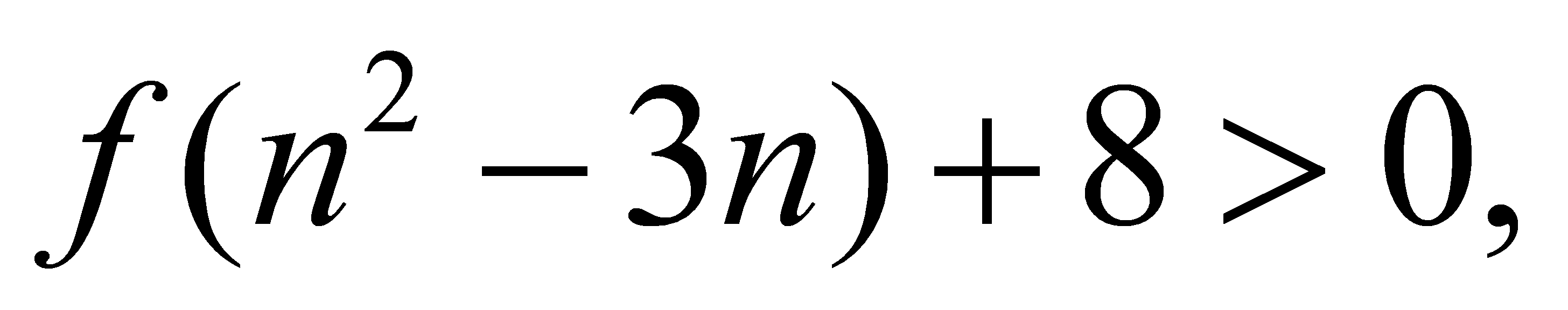
即为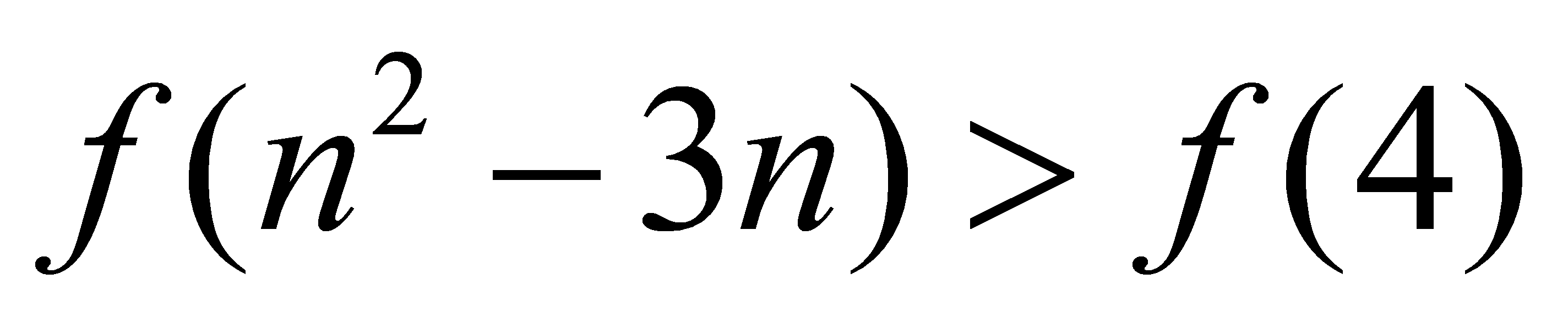 ,因为
,因为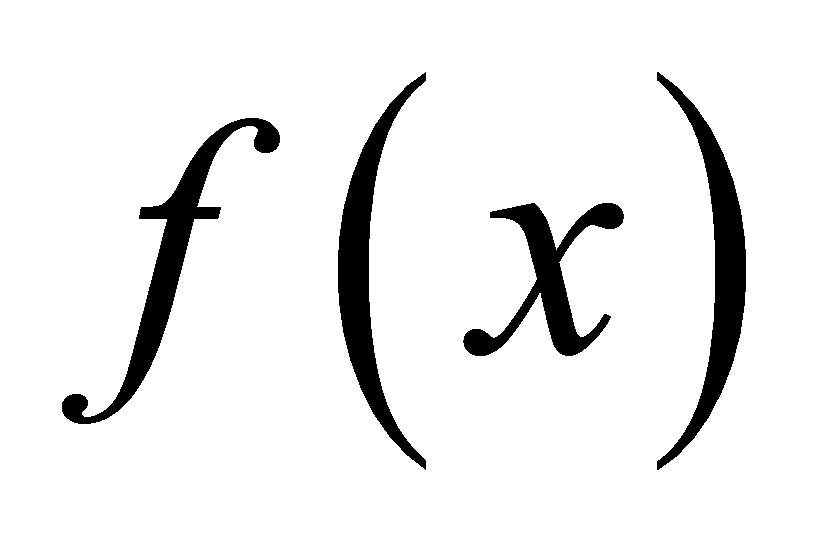 在
在 上单调递减
上单调递减
所以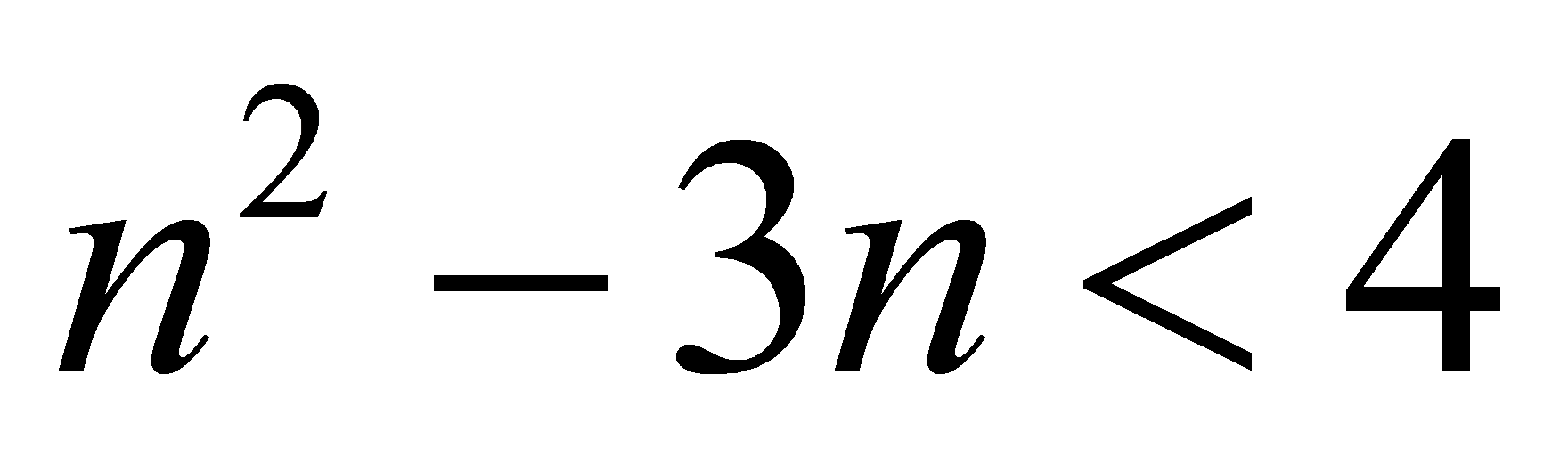 ,所以
,所以 ,所以
,所以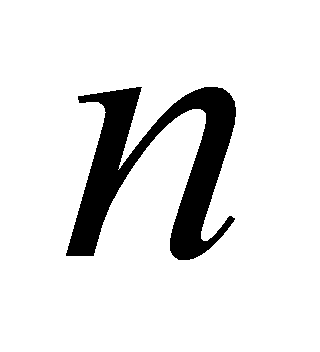 的取值范围是
的取值范围是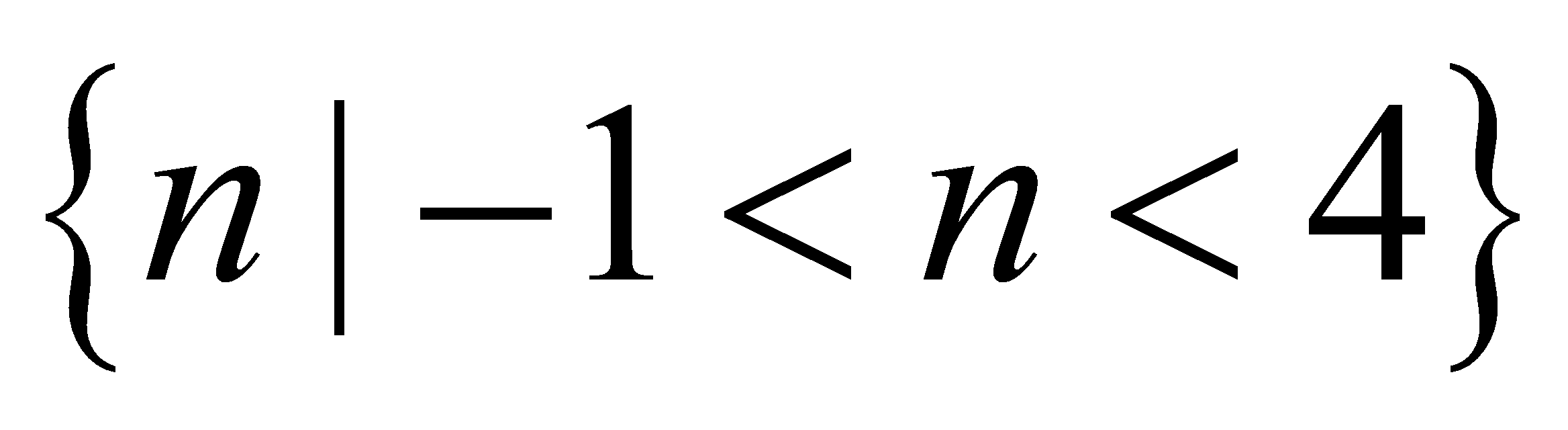
18.
解:(1)∵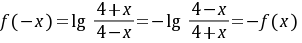 ,
,
∴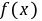 是奇函数.
是奇函数.
(2) 在
在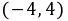 上为减函数.
上为减函数.
证明:任取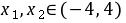 且
且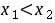 ,
,
则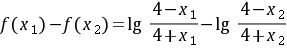
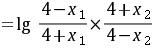
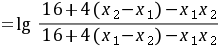 ,
,
∵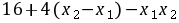
 ,
,
∴ ,
,
得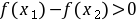 ,得到
,得到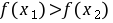 ,
,
∴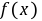 在
在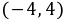 上为减函数;
上为减函数;
(3)∵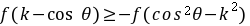
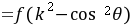 ,
,
∵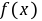 在
在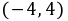 上为减函数,
上为减函数,
∴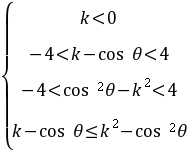 对
对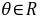 恒成立
恒成立
由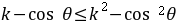 对
对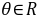 恒成立得:
恒成立得:
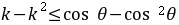 对
对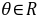 恒成立,
恒成立,
令 ,
,
∵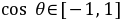 ,∴
,∴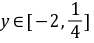 ,
,
∴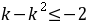 ,得
,得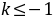 ,
,
由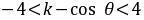 对
对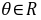 恒成立得:
恒成立得:
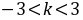 ,由
,由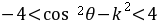 对
对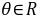 恒成立得:
恒成立得: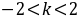 ,
,
即综上所得: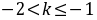 ,
,
所以存在这样的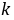 ,其范围为
,其范围为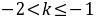 .
.
19.
(Ⅰ)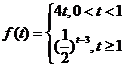
(Ⅱ)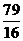 小时
小时
20.
(1)当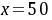 时,此时甲城市投资50万元,乙城市投资70万元
时,此时甲城市投资50万元,乙城市投资70万元
所以总收益 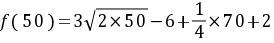 =43.5(万元) ……………4分
=43.5(万元) ……………4分
(2)由题知,甲城市投资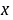 万元,乙城市投资
万元,乙城市投资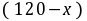 万元 ……………5分
万元 ……………5分
所以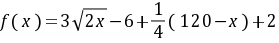
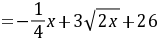
依题意得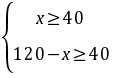 ,解得
,解得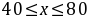
故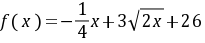
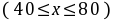 ……………8分
……………8分
令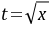 ,则
,则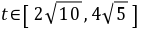
所以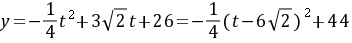
当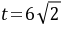 ,即
,即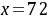 万元时,
万元时, 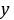 的最大值为44万元 ……………11分
的最大值为44万元 ……………11分
故当甲城市投资72万元,乙城市投资48万元时,
总收益最大,且最大收益为44万元 ……………12分
21.
解:(1)因为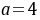 ,
,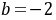 ,所以
,所以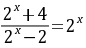 ,
,
化简得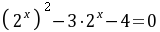 ,解得
,解得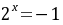 (舍)或
(舍)或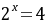 ,
,
所以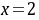 .
.
(2)因为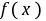 是奇函数,所以
是奇函数,所以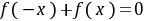 ,所以
,所以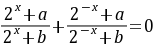 ,
,
化简变形得: ,
,
要使上式对任意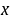 的成立,则
的成立,则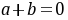 且
且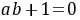 ,
,
解得: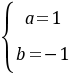 或
或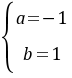 ,因为
,因为 的定义域是
的定义域是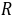 ,所以
,所以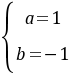 舍去,
舍去,
所以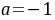 ,
,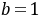 ,所以
,所以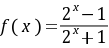 .
.
①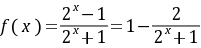
对任意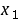 ,
,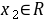 ,
,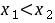 有:
有: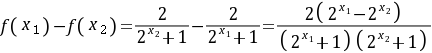 ,
,
因为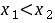 ,所以
,所以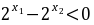 ,所以
,所以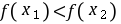 ,
,
因此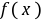 在
在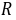 上递增,
上递增,
因为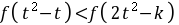 ,所以
,所以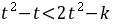 ,
,
即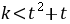 在
在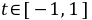 时有解,
时有解,
当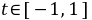 时,
时,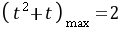 ,所以
,所以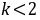 .
.
②因为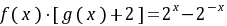 ,所以
,所以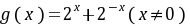 ,
,
所以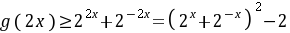 ,
,
不等式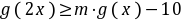 恒成立,即
恒成立,即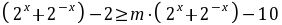 ,
,
令 ,
,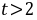 ,则
,则 在
在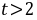 时恒成立,
时恒成立,
因为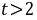 ,由基本不等式可得:
,由基本不等式可得: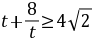 ,当且仅当
,当且仅当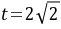 时,等号成立,
时,等号成立,
所以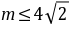 ,则实数
,则实数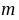 的最大值为
的最大值为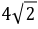 .
.